Thermodynamic integration and umbrella sampling are methods to calculate the free-energy change of chemical reactions. In a special case of the former, the reaction coordinate is constrained to specific values and the force of constraint is sampled. In the latter, a harmonic bias is applied to keep the reaction coordinate near a specified value. This is done in a number of windows along the reaction coordinate. The combination of the windows allows to calculate the free-energy change along the reaction coordinate. Umbrella sampling simulations are traditionally analyzed using the weighted histogram analysis method (WHAM). In most cases, UI is advantageous over WHAM [1]. In UI, the derivative of the free energy with respect the the reaction coordinate (mean force) is calculated in each window. This derivative (but not the free energy itself) can be averaged over the windows. Integration yields the free energy.
Umbrella integration can be performed in one [1] or more [3] reaction coordinates. Usually, a truncation of a Taylor series after the quadratic term is done. Higher-order terms are available, though [4]. The minimum free-energy path of a reaction can be found with different methods, among those is umbrella integration [5,6].
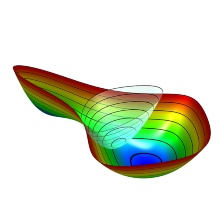
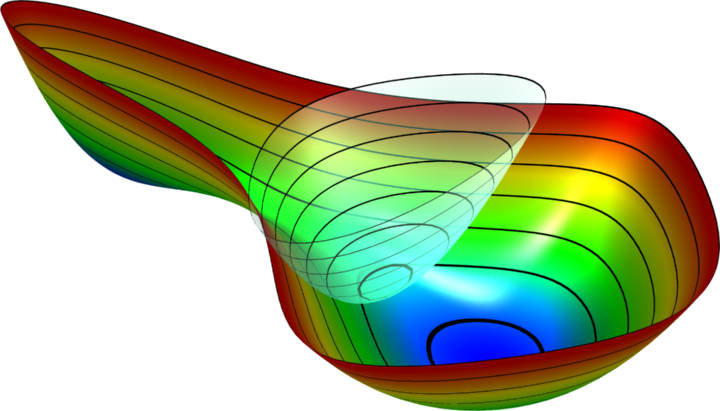
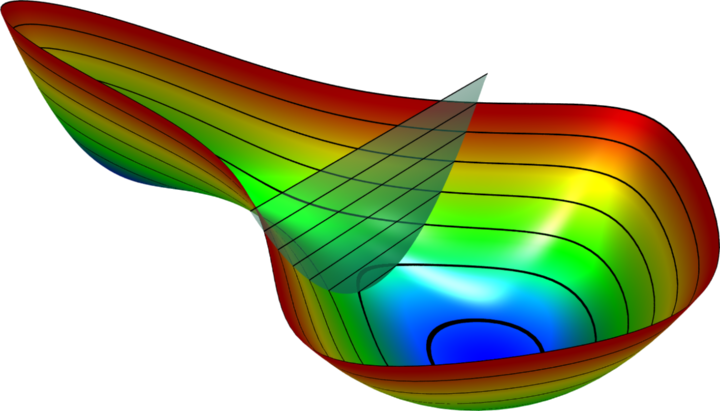
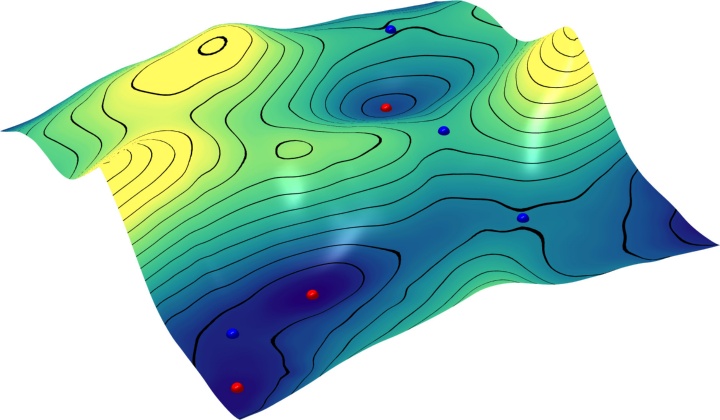
The colorful pictures on the right are potential energy surfaces. In the top picture, the biased potential of umbrella integration (UI) is inserted. The plane in the middle picture indicates the value of the reaction coordinate to which the system is constrained in thermodynamic integration. The bottom picture is a two-dimensional free-energy surface from [3].
Code to perform umbrella integration analysis is available for free upon request.