Ich beschäftige mich nicht mit dem, was getan worden ist. Mich interessiert, was getan werden muss.
Marie Curie
Aktuelle Forschungsprojekte
Derzeit werden bei uns im Einzelnen die im Folgenden aufgelisteten Forschungsprojekte bearbeitet.
Working Platforms: A comparison of the available design methods coupled with practical design approaches and validation in the field
RES:Z - Verbundvorhaben: IWAES - Integrative Betrachtung einer nachhaltigen Wärmebewirtschaftung von Stadtquartieren im Stadtentwicklungsprozess
Die Forschungsprojekte der Fördermaßnahme „Ressourceneffiziente Stadtquartiere für die Zukunft – RES:Z“ des Bundesministeriums für Bildung und Forschung (BMBF) erarbeiten Konzepte für den ressourceneffizienten Umgang mit Wasser, Fläche, Stoffströmen, Energie und Stadtgrün in urbanen Gebieten. Das Ziel ist eine integrative Planung und ein auf Nachhaltigkeit ausgerichtetes Management von Stadtquartieren mit Beteiligung und Abstimmung aller relevanten Akteuren.
Das inter- und transdisziplinäre Verbundprojekt IWAES verfolgt das Ziel, durch einen innovativen, ganzheitlichen Ansatz Infrastruktursysteme der Siedlungswasserwirtschaft zur Ein- und Ausspeicherung von Wärme- und Kälteenergie innerhalb eines Stadtquartiers unter integrativer Betrachtung von Stadtentwicklungsprozessen zu adaptieren, um so die Grundlage für einen ausgeglichenen Wärmehaushalt im urbanen Umfeld zu schaffen.
IWAES stellt die zentralen Themen der Richtlinie „Ressourcen-effiziente Stadtquartiere für die Zukunft“ Wasserwirtschaft und Flächennutzung in den Fokus der Bearbeitung. Hierbei sind folgende Fragestellungen zu beantworten:
- Kann durch eine technische und stadtplanerische Optimierung ein ausgeglichener Wärme-/Kältehaushalt
innerhalb eines Stadtquartiers erreicht werden? - Wie sieht eine effiziente und technisch realisierbare Infrastruktur zur Verteilung und Speicherung der
Wärmeenergie unter Nutzung der Konstruktionen des Siedlungswasserbaus aus?
Das Institut für Geotechnik der Universität Stuttgart (IGS) übernimmt im Rahmen dieses Projektes die Gesamtkoordination sowie die Modellierung des Wärmeverbundnetzes nebst den Detailuntersuchungen des adaptierten thermisch aktivierten Hybridkanals.
Förderkennzeichen
033W106A (IWAES)
033W106AN (IWAES II)
Laufzeit
01.04.2019 bis 30.09.2022 (IWAES)
01.11.2022 bis 31.10.2024 (IWAES II)
Bearbeiter
Till Kugler / Matin Liaghi
VISSKA - Messung, Modellierung und Bewertung der Vibrationsrammung in Bezug auf Installation, Schallemissionen und Auswirkungen auf Schweinswale im Offshore-Windpark KASKASI II
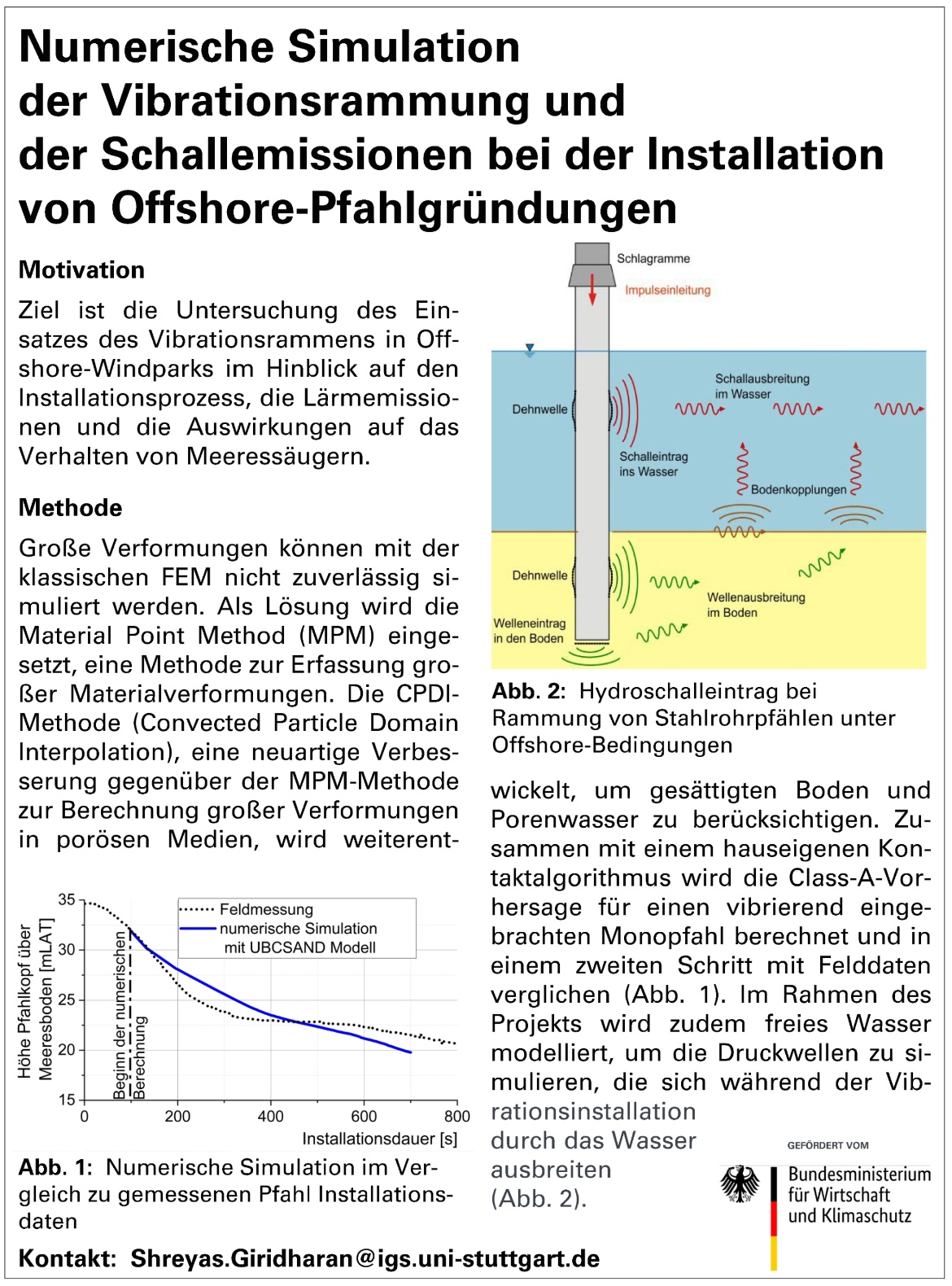
Zusammen mit den vier Projektpartnern knüpft das Institut für Geotechnik der Universität Stuttgart (IGS) mit diesem Vorhaben an jahrelange Forschung im Bereich der Vibrationsrammung als Gründungsmethode für Offshore-Fundamente im Labor und in Feldversuchen an. Die bisher durchgeführten Untersuchungen haben bereits gezeigt, dass das Installationsverfahren das Potenzial hat, sowohl die Unterwasserschallemissionen als auch die Installationsdauer zu verringern. Ziel dieses Forschungsprojekts ist es, auf den vorliegenden Ergebnissen aufzubauen und diese um weitere Erkenntnisse zu ergänzen. Langfristig soll die neuartige Gründungsmethode als eine schallärmere und naturverträglichere Alternative zum bisher genutzten Impulsrammverfahren etabliert werden.
Das Projekt wird begleitend zur Errichtung des Offshore-Windparks „KASKASI II“ durchgeführt. Durch die Entwicklung und Validierung von Prognosemodellen zur Einbringbarkeit und zur Schallentwicklung sowie durch die Untersuchung der Reaktion von Schweinswalen auf den Dauerschall soll die Überführung des neuartigen Installationsverfahrens in den Stand der Technik ermöglicht werden.
Zentrales Ziel des vom Institut für Geotechnik der Universität Stuttgart (IGS) bearbeiteten Teilvorhabens ist die Fortentwicklung und Validierung eines numerischen Simulationsmodells, das durch eine physikalisch begründete Modellbildung die Ermittlung und Prognose des Eindringverhaltens sowie der dabei entstehenden Unterwasserschallemissionen bei der Vibrationsrammung von Monopiles bei zukünftigen Windpark-Projekten unter Berücksichtigung der standortspezifischen Baugrundverhältnisse und der gewählten Herstellparameter ermöglicht.
Förderkennzeichen
03EE3043D
Laufzeit
01.01.2021 bis 30.04.2023
Bearbeiter
Shreyas Giridharan / Sujith Gowda / Bastian Hoffmann
BOROPLAST ® - "Ideale Bohrlochverfüllung"
Mechanisches Verhalten und Dauerhaftigkeit von Bohrlochverfüllungen unter nicht-monotonen Einwirkungen aus Eisenbahnverkehr bei Einsatz schüttfähiger und verdichtbarer Verfüllmaterialien auf Basis von Quelltonen
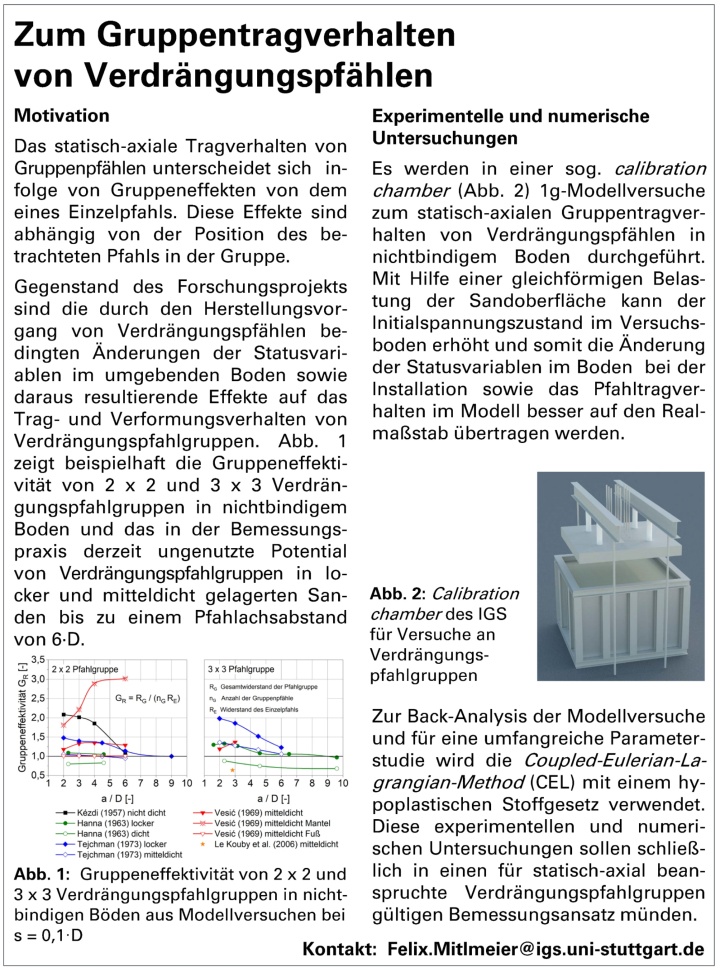
Beurteilung des Trag- und des Verformungsverhaltens von Dauerbodennägeln unter besonderer Betrachtung des Beanspruchungszustandes der Zementsteinumhüllung im Gebrauchszustand - Internationale Literaturstudie
Förderkennzeichen
P 52-5-11.80-2081/21
Laufzeit
01.06.2021 bis 30.11.2021
Bearbeiter
Optimierung der Bemessung von unbewehrten und bewehrten Tragschichten für mobile Baumaschinen
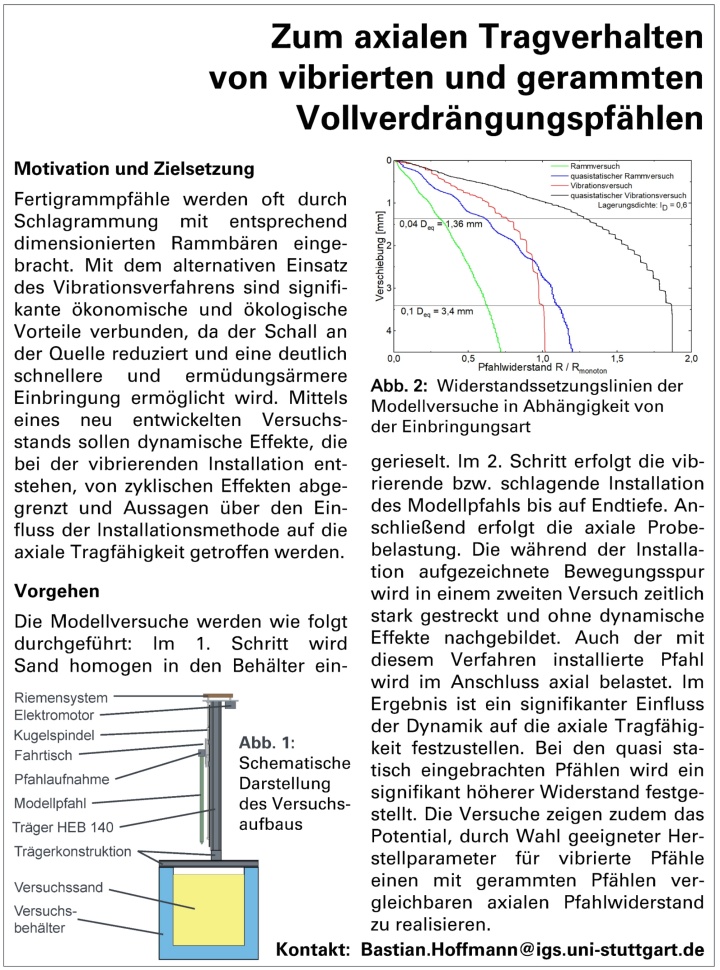
Zum axialen Tragverhalten von vibrierten und gerammten Vollverdrängungspfählen
Scaled Testing of Vibration in Medium to Dense Sands
Bearbeiter
Johannes Labenski / Bastian Hoffmann
Förderkennzeichen
Vibro Café
Laufzeit
01.01.2018 bis 28.02.2019
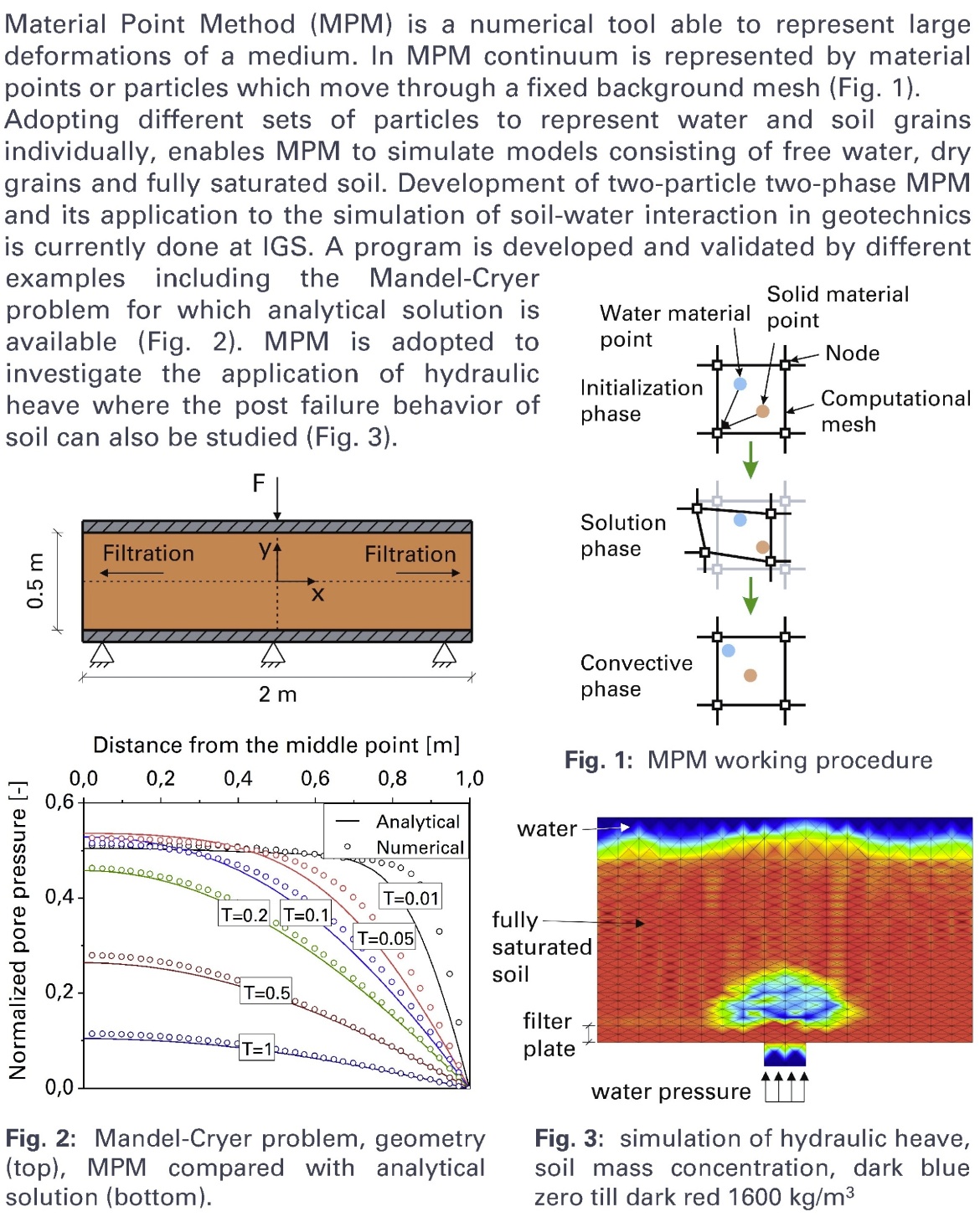
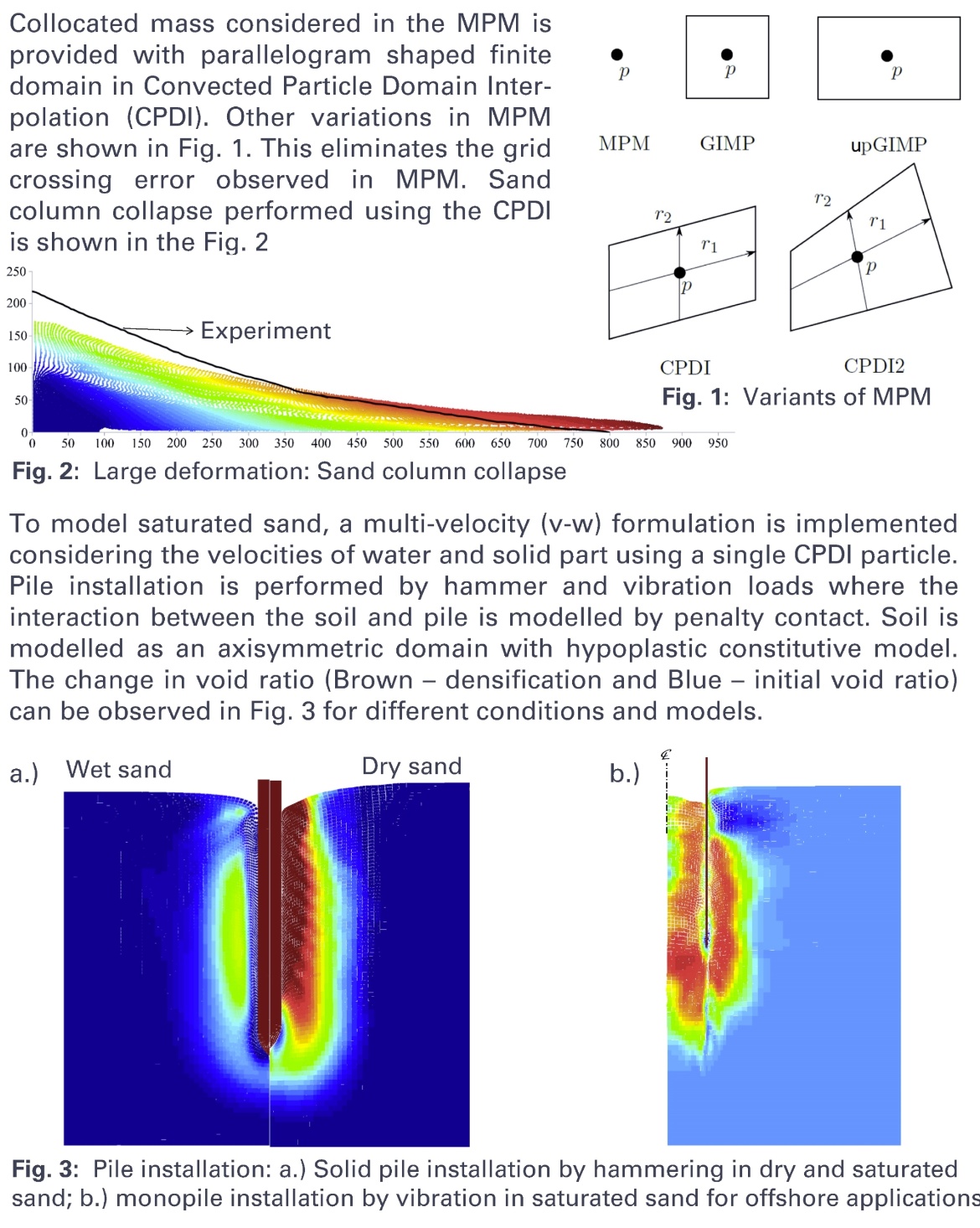
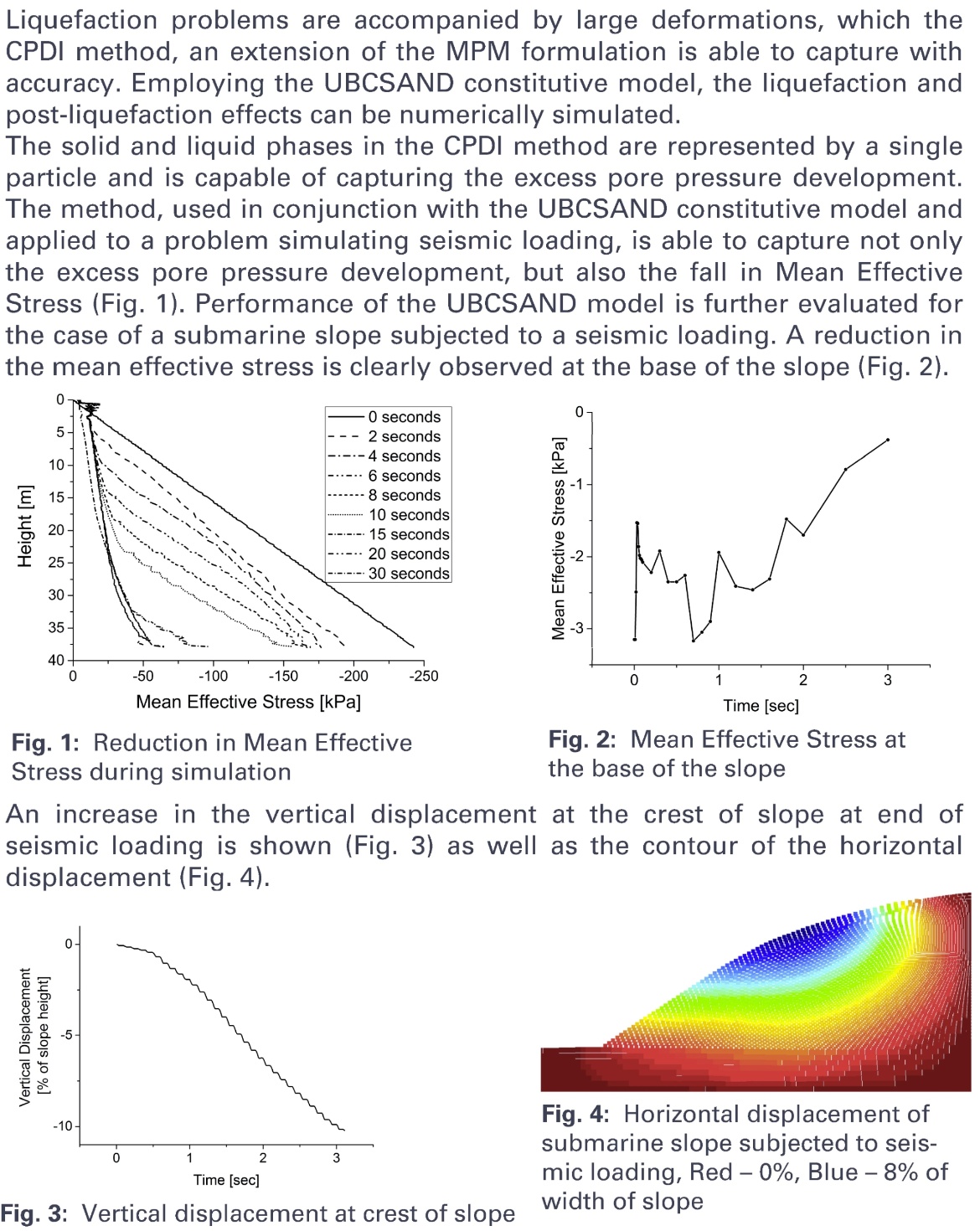
Formulation and implementation of two-phase Material Point Method
Bearbeiter: Seyedfarzad Fatemizadeh
Pile installation using CPDI
Bearbeiter: Sujith Gowda
Liquefaction simulation using CPDI
Bearbeiter: Shreyas Giridharan



 EFFC/DFI Working Platforms Task Group
EFFC/DFI Working Platforms Task Group European Federation of Foundation Contarctor
European Federation of Foundation Contarctor